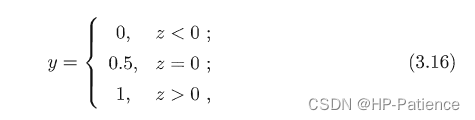所需数学知识

求偏导
矩阵求导
求逆矩阵

名词解释

1.序关系

有序：属性之间可进行相对比较（如大、中、小）
无序：属性之间不可进行相对比较（如南瓜、西瓜、冬瓜）

2.符号arg与s.t.

arg：即argument（参数），用于表示求出指定函数时的**参数取值**
	例如：
	arg min 就是使后面这个式子达到最小值时的 变量的取值
	arg max 就是使后面这个式子达到最大值时的 变量的取值
	
s.t.：即subject to，意思是受限于...，后面紧跟约束条件

3.闭式解

也叫做 解析解，
闭式解就是一些严格的公式,给出任意的自变量就可以求出其因变量,也就是问题的解
南瓜书中说闭式解是指可以通过具体的表达式解出待解参数

模型介绍

表示形式

对于拥有d个属性的示例 x，表示为：$$x = ( x _ { 1 } ; x _ { 2 } ; \ldots ; x _ { d } )$$
其中$x_i$表示第i个属性的属性值
而我们将各属性的线性组合作为线性模型，表示为：
$$ f ( x ) = w _ { 1 } x _ { 1 } + w _ { 2 } x _ { 2 } + \ldots + w _ { d } x _ { d } + b $$

也可写成向量形式 $$ f ( x ) = w ^ { T } x + b ,$$ 其中$w$和$x$均为列向量，其中$w$可以理解成为不同属性的**偏好**而赋予的**权重** 故线性模型具有很强的**可解释性**

模型优点

简单（模型表示、数学公式简单）
基本（通过引入层级结构或高维映射可以得到许多非线性模型）
可理解性好（通过权重可以看出对属性的偏好）

属性数值化

总结：离散属性的处理：若有“序”(order)，则连续化；否则，转化为 𝑘维向量

对于线性模型的求解，我们首先需要明确参数的输入和求解两个部分

我们知道模型的输入为各个示例 $x_i$，其中的$x_i$由d个属性组成，而我们用d个属性值表示一个具体的示例$x_i$作为输入

这时我们会发现我们需要注意属性值的数据类型
于是这里我们把属性分为两类

连续属性
离散属性
- 有序的离散属性
- 无序的离散属性

对于有序的属性，我们用相对值表示属性值，如大、中、小分别用1，0.5，0来表示

对于无序的属性，我们用0/1表示属性值，我们记改属性有m种属性值，则一个属性值需要m维列向量进行表示。

比如对于属性瓜的类别，有西瓜，南瓜，冬瓜三种属性值，则表示为
$$ x _ { 1 } = ( 1 ; 0 ; 0 ) , x _ { 2 } = ( 0 ; 1 ; 0 ) , x _ { 3 } = ( 0 ; 0 ; 1 ) $$
这里表示示例$x_1,x_2,x_3$分别为西瓜，南瓜，冬瓜

对于回归，二分类，多分类任务，我们给出不同的线性模型

![[西瓜书学习/西瓜书-第3章/1.png]]

回归任务

最小二乘法

在第二章中我们知道均方误差是回归任务的常见性能度量
均方误差本身也具有很好的几何意义，对于欧氏距离

定义：基于均方误差最小化进行模型求解，使得样本到直线的欧式距离之和最小

数学知识：涉及求偏导数

1.一元线性回归

1.假设方程 $$ f\left(x_{i}\right)=w x_{i}+b, 使得 f\left(x_{i}\right) \simeq y_{i}. $$ 2.均方误差最小化时的w和b的值 $$ \begin{aligned}\left(w^{*}, b^{*}\right) & =\underset{(w, b)}{\arg \min } \sum_{i=1}^{m}\left(f\left(x_{i}\right)-y_{i}\right)^{2} \\ & =\underset{(w, b)}{\arg \min } \sum_{i=1}^{m}\left(y_{i}-w x_{i}-b\right)^{2} .\end{aligned} $$ 3.均方误差对𝑤与𝑏求偏导 $$ \begin{array}{l}\frac{\partial E_{(w, b)}}{\partial w}=2\left(w \sum_{i=1}^{m} x_{i}^{2}-\sum_{i=1}^{m}\left(y_{i}-b\right) x_{i}\right), \\ \frac{\partial E_{(w, b)}}{\partial b}=2\left(m b-\sum_{i=1}^{m}\left(y_{i}-w x_{i}\right)\right),\end{array} $$ 此处$E_{(w, b)}$是是关于w和b的凸函数 **注意**：此处凸函数定义与数学分析中相同，与高等数学中相反 4.令偏导为0，得到闭式解，解得w和b $$ \begin{array}{c}w=\frac{\sum_{i=1}^{m} y_{i}\left(x_{i}-\bar{x}\right)}{\sum_{i=1}^{m} x_{i}^{2}-\frac{1}{m}\left(\sum_{i=1}^{m} x_{i}\right)^{2}}, \\ b=\frac{1}{m} \sum_{i=1}^{m}\left(y_{i}-w x_{i}\right)\end{array} $$

2.多元线性回归

额外数学知识:

矩阵求导

基于本人数学系所教授的高等代数中无此内容，故认为需要额外补充学习

详见西瓜书附录P400 A.2 导数

1.假设方程 $$ f\left(\boldsymbol{x}_{i}\right)=\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}+b, 使得 f\left(\boldsymbol{x}_{i}\right) \simeq y_{i}, $$ 2.为便于讨论，把w和b吸收入向量形式，数据集表示为

$$
\mathbf{X}=\left(\begin{array}{ccccc}x_{11} & x_{12} & \ldots & x_{1 d} & 1 \ x_{21} & x_{22} & \ldots & x_{2 d} & 1 \ \vdots & \vdots & \ddots & \vdots & \vdots \ x_{m 1} & x_{m 2} & \ldots & x_{m d} & 1\end{array}\right)=\left(\begin{array}{cc}\boldsymbol{x}{1}^{\mathrm{T}} & 1 \ \boldsymbol{x}{2}^{\mathrm{T}} & 1 \ \vdots & \vdots \ \boldsymbol{x}_{m}^{\mathrm{T}} & 1\end{array}\right)
$$
示例中的属性值为列向量，同时将标记写成向量形式 $y = ( y _ { 1 } ; y _ { 2 } ; \ldots ; y _ { m } )$

注意：此处将$f\left(\boldsymbol{x}{i}\right)=\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}{i}+b$中的 $b$ 拆成b*1的形式，用$x$吸收$1$，用$w$吸收$b$变成$\hat{\boldsymbol{w}}$

![[西瓜书学习/西瓜书-第3章/2.png]]
[图片源于周志华老师]

3.解得w $$ \hat{\boldsymbol{w}}^{*}=\left(\mathbf{X}^{\mathrm{T}} \mathbf{X}\right)^{-1} \mathbf{X}^{\mathrm{T}} \boldsymbol{y} $$ 4.最终解得模型为： $$ f\left(\hat{\boldsymbol{x}}_{i}\right)=\hat{\boldsymbol{x}}_{i}^{\mathrm{T}}\left(\mathbf{X}^{\mathrm{T}} \mathbf{X}\right)^{-1} \mathbf{X}^{\mathrm{T}} \boldsymbol{y}. $$

$1.若 X ^ { T } X 满秩或正定 , 则 w ^ { * } = ( X ^ { T } X ) ^ { - 1 } X ^ { T } y$
$2.若X ^ { T } X 不满秩 , 则可解出多个 \widehat { w }$
此时需求助于归纳偏好，常见做法是引入 正则化项（详见6.4节，11.4节）

通过在损失函数中添加惩罚项来限制模型的复杂度，常见的正则化方法包括岭回归（Ridge Regression）、Lasso回归和弹性网（Elastic Net）

PS：$\widehat { w } ^ { * }$转换成二次型矩阵相乘还挺有意思的，推导详见南瓜书P35，P36

3.广义线性模型(GLM)

令预测值逼近 y 的衍生物

对数线性模型

假设我们认为示例所对应的输出标记是在指数尺度上变化，那就可将输出标记的对数作为线性模型逼近的目标

个人理解：

其实就是我们在原样本中，通过数值或者散点图，观察到输出标记在指数尺度上变化，故很难直接用一条直线拟合输出标记，因为标记值本身为非线性增长。

而对在指数尺度上变化的输出标记取对数后，就可以将输出标记映射到线性尺度上变化，故易于用直线拟合

$$ y = w ^ { T } x + b $$

将输出标记 y 取对数转变为形式上的线性回归方程

$$ \ln y = w ^ { T } x + b $$

实际上是在试图让$e ^ { w ^T x} + b$逼近y

这里的对数函数起到了将线性回归模型的预测值与真实标记联系起来的作用

但实质上已是在求取输入空间到输出空间的非线性函数映射

我们知道，对数线性模型是使用对数函数将输出标记进行映射

那么如果我们选取不同的函数对输出标记进行映射，就能将一个非线性变化的样本用线性模型进行拟合了。

而此时问题就转变为映射函数的寻找了，需要找到一个合适的映射函数，将原来的标记值数据形态映射成线性的🤔

这里就涉及到模型的优化了，找到映射函数得到新的线性模型，并在某一性能度量下进行比较，结合需求选择模型。

而由此我们引出了广义线性模型（Generalized Linear Model）的定义：

$$ y = g ^ { - 1 } ( w ^ { T } x + b )$$
其中$g ( \cdot )$为连续且充分光滑的单调可微函数，称为联系函数(link function)

广义线性模型的参数估计常通过加权最小二乘法或极大似然法进行

显然，对数线性回归是广义线性模型在 $g ( \cdot )$=$ln ( \cdot )$时的特例显然，一元线性回归也是如此

分类任务

引导

在先前的文章：西瓜书-第3章-线性模型 (Part 1) 中我们介绍了一元线性回归、多元线性回归、广义线性回归（对数线性回归）的模型,
用于解决回归类问题

那么对于分类问题，我们又该使用哪种模型呢？我们知道分类问题可以分成二分类与多分类问题

此处我们先介绍二分类问题所使用的模型

我们刚学过回归类问题的模型，此时我们运用广义线性回归的思想，只要我们能找到一个联系函数，能够将连续值变成离散值，即可将回归类模型运用到分类问题上。

对数几率回归

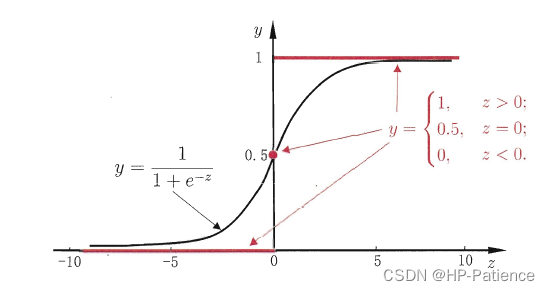
这里我们先给出“单位阶跃函数“(unit-step function)

此函数能够将输出范围在R上的标记转换为离散值

若预测值大于零就判为正例，小于零则判为反例，预测值为临界值零则可任意判别

在这里插入图片描述
我们可以看出这个函数的效果是很不错的但是因为其函数性质很差，不连续也不可微，不符合联系函数的定义

所以我们引进了对数几率函数，简称“对率函数”
$$ y = \frac { 1 } { 1 + e ^ { - z } } .$$
故有
$$ \ln \frac { y } { 1 - y } = w ^ { T } x + b .$$
在这里插入图片描述

1	若将y 视为样本x 作为正例的可能性，则1 - y 是其反例可能性,两者的比值称为“几率”(odds),反映了x作为正例的相对可能性。

最小二乘法仅可解决凸函数的问题，并对于高阶函数不易用，而且对于多元回归的函数，矩阵可能无法求逆，因为其可能是不满秩的(奇异矩阵/非正定矩阵)

故我们通过极大似然法+梯度下降法进行求解